「CF715D」Create a Maze

发表于 | 更新于 | 分类于 | 阅读次数：

神仙构造题不是人能场上做出来的……

[CF 715D]

题意简述

一个四联通的 $n\times m$ 的迷宫，相邻的两个位置之间可能有墙阻隔使得这两个位置不能直接互达，一共有 $k$ 堵墙。从 $(1,1)$ 进入迷宫，而出口是 $(n,m)$ ，假设现在在 $(x,y)$ ，下一步只能走到 $(x + 1,y)$ 或 $(x,y + 1)$ ，当然不能走出迷宫且下一步走到的位置和现在位置之间不能有墙。通过一些计算，得出从入口 $(1,1)$ 走到 $(n,m)$ 共有 $T$ 种走法。

现在给出 $T$ ， $1\le T\le 10^{18}$ ，希望你构造出一个迷宫，使得从入口 $(1,1)$ 走到 $(n,m)$ 共有 $T$ 中走法，限制 $1\le n,m\le 50, 0\le k\le 300$ 。

主要思路

考虑在 $(x,y)$ 时答案是 $T$ 。发现可以简单地在 $(x+1,y+1)$ 获得 $2T$ 。

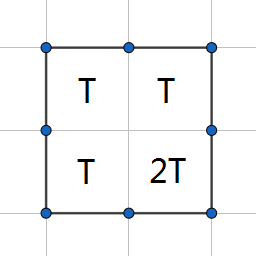
CF715D_01

如何将 $T$ 变为 $2T + 1$ ？考虑将上方开一小口，将一个 $1$ 引入。

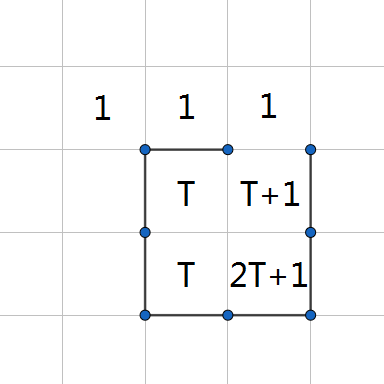
CF715D_02

如何保证引入的是 $1$ ？

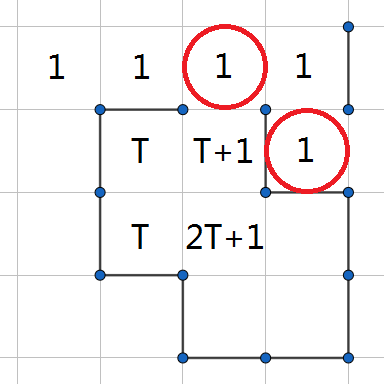
CF715D_03

发现只需要保证红圈位置的为 $1$ 即可，所以可以在外面建墙。

那么初始的状态如何生成呢？如图，左上角为 $(1,1)$ 。

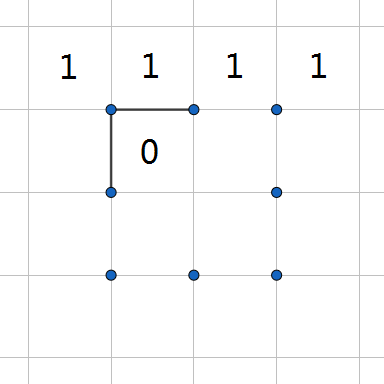
CF715D_05

这样，可以将 $T$ 转换成二进制数，就可以得到 $T < 2^{50}$ 的做法了。



然而题目要求做到 $T \le 10^{18}$ ，如何解决？

发现可以在 $(x+2,y+2)$ 获得 $6T$ ，而 $6 > 2^2$ ，看起来就可以将 $n,m$ 卡进 $50$ 以内。

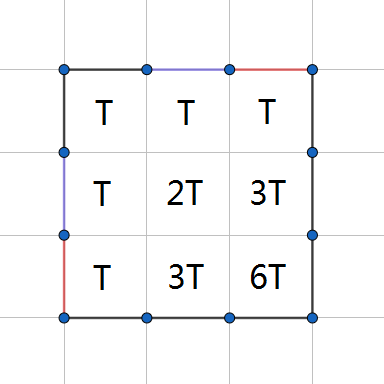
CF715D_04

但是我们同时要便于获得 $6T + i$ ( $1\le i \le 5$ )。

发现在引入 $1$ 的情况下，若不建图中的蓝墙，不建一堵墙会增加 $3$ 种方案；不建图中的红墙，不建一堵墙会增加 $1$ 种方案。如此就可以将 $T$ 转换成六进制做了。

同时为了保证引入的是 $1$ ，可以如图所示在外围建墙。此时，计算最大的 $n,m,k$ ，发现都可以卡进限制范围内。

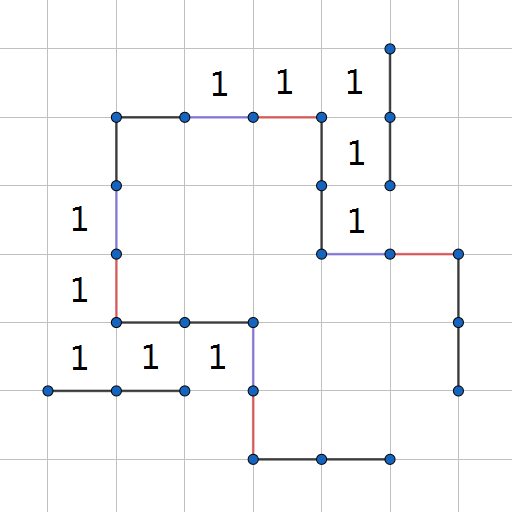
CF715D_06

初始状态同二进制做法。

参考代码

代码写起来特别难受……
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include<bits/stdc++.h>
namespace my_std{
    using namespace std;
    #define reg register
    #define Rint register int
    #define FOR(i,a,b) for(register int i=(a),ed_##i=(b);i<=ed_##i;++i)
    #define ROF(i,a,b) for(register int i=(a),ed_##i=(b);i>=ed_##i;--i)
    #define FORit(templ,arr,i,a,b) for(register templ *i=(arr)+(a),*ed_##i=(arr)+(b)+1;i!=ed_##i;++i)
    #define ROFit(templ,arr,i,a,b) for(register templ *i=(arr)+(a),*ed_##i=(arr)+(b)-1;i!=ed_##i;--i)
    #define GO(x,p,e,i,v) for(register int i=p[x].head,v;i;i=e[i].link)
    #define MEM(x,v) memset(x,v,sizeof(x))
    #define fir first
    #define sec second
    #define pq priority_queue
    #define MP make_pair
    typedef long long LL;
    typedef double DB;
    typedef pair<int,int> PII;
    #define Templ(T) template<typename T>
    inline LL read(){
        reg LL ans=0,f=1;reg char c=getchar();
        while(!isdigit(c)){ f^=(c=='-'); c=getchar(); }
        for(;isdigit(c);c=getchar()) ans=ans*10+c-'0'; return f?ans:-ans;
    }
    Templ(_Tp) inline int chkmin(_Tp &x,_Tp y){ return x>y?x=y,1:0; }
    Templ(_Tp) inline int chkmax(_Tp &x,_Tp y){ return x<y?x=y,1:0; }
    #define using_mod
    const int mod = 998244353, K = 310, N = 55;
    #ifdef using_mod
    inline void inc(int &x,const int &y){ x+=y; if(x>=mod) x-=mod; }
    inline int ksm(int x,LL y){ int res=1; for(;y;y>>=1,x=1ll*x*x%mod) if(y&1) res=1ll*res*x%mod; return res;}
    #endif
    Templ(_Tp) inline _Tp gcd(_Tp x,_Tp y){ return y?gcd(y,x%y):x; }
    #define FILE(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)
    #define PBTXDY
}
using namespace my_std;

LL T;
struct Wall{
    int x, y, xx, yy;//x <= xx, y <= yy
}Q[K];
int top, a[N], acnt;

int main(){
    T = read();
    while(T){
        a[acnt++] = T % 6;
        T /= 6;
    }
    FOR(i, 0, (acnt - 1) >> 1) swap(a[i], a[acnt - 1 - i]);
    Rint n = 2;
    Q[top++] = (Wall){ 1, 2, 2, 2 }, Q[top++] = (Wall){ 2, 1, 2, 2 };
    FOR(i, 0, acnt - 1){
        if(n > 2){
            Q[top++] = (Wall){ n - 2, n + 2, n - 1, n + 2 }, Q[top++] = (Wall){ n + 2, n - 2, n + 2, n - 1 };
            if(i != acnt - 1){
                Q[top++] = (Wall){ n - 2, n + 3, n - 1, n + 3 }, Q[top++] = (Wall){ n + 3, n - 2, n + 3, n - 1 };
            }
        }
        if(i != acnt - 1){
            Q[top++] = (Wall){ n, n + 2, n, n + 3 }, Q[top++] = (Wall){ n + 1, n + 2, n + 1, n + 3 };
            Q[top++] = (Wall){ n + 2, n, n + 3, n }, Q[top++] = (Wall){ n + 2, n + 1, n + 3, n + 1 };
        }
        switch(a[i]){
            case 0 :{
                Q[top++] = (Wall){ n - 1, n + 1, n, n + 1 }, Q[top++] = (Wall){ n - 1, n + 2, n, n + 2 };
                Q[top++] = (Wall){ n + 1, n - 1, n + 1, n }, Q[top++] = (Wall){ n + 2, n - 1, n + 2, n };
                break;
            }
            case 1 :{
                Q[top++] = (Wall){ n - 1, n + 1, n, n + 1 };
                Q[top++] = (Wall){ n + 1, n - 1, n + 1, n }, Q[top++] = (Wall){ n + 2, n - 1, n + 2, n };
                break;
            }
            case 2 :{
                Q[top++] = (Wall){ n - 1, n + 1, n, n + 1 };
                Q[top++] = (Wall){ n + 1, n - 1, n + 1, n };
                break;
            }
            case 3 :{
                Q[top++] = (Wall){ n - 1, n + 2, n, n + 2 };
                Q[top++] = (Wall){ n + 1, n - 1, n + 1, n }, Q[top++] = (Wall){ n + 2, n - 1, n + 2, n };
                break;
            }
            case 4 :{
                Q[top++] = (Wall){ n + 1, n - 1, n + 1, n }, Q[top++] = (Wall){ n + 2, n - 1, n + 2, n };
                break;
            }
            case 5 :{
                Q[top++] = (Wall){ n + 1, n - 1, n + 1, n };
                break;
            }
        }
        n += 2;
    }
    printf("%d %d %d\n", n, n, top);
    FORit(Wall, Q, i, 0, top - 1){
        printf("%d %d %d %d\n", i->x, i->y, i->xx, i->yy);
    }
    return 0;
}

其他解法

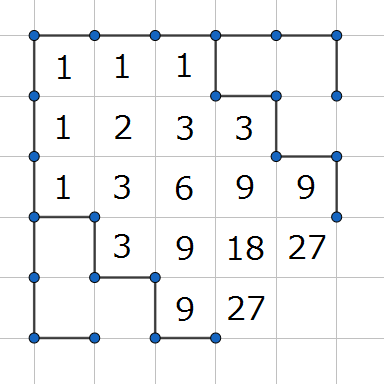
CF715D_07

如图，可以将 $T$ 转化为三进制做，一位是几就把那一位对应的几面墙打开，外面的墙是用于将答案引至最终点的。

据说这样更好写？