调和太有意思了,所以就有了这篇博客。
基本定义
调和点列
【定义1.1】
对于线段 $AB$ 的内分点 $C$ 和外分点 $D$,若满足 $\dfrac{AC}{BC}=\dfrac{AD}{BD}$,即内分比等于外分比,则称点 $C, D$ 调和分割线段 $AB$,或者点 $A, B, C, D$ 为调和点列。
若直线 $l$ 上,点 $C, D$ 调和分割线段 $AB$,$M$ 为 $AB$ 中点,则有:
【性质1.1】
点 $A, B$ 调和分割线段 $CD$。
【性质1.2】
$\dfrac{1}{AC} + \dfrac{1}{AD} = \dfrac{2}{AB}$。
【性质1.3】
$AB\cdot CD = 2AD\cdot BC$。
【性质1.4】
$CA\cdot CB = CM\cdot CD$,$DA\cdot DB = DM\cdot DC$。
【性质1.5】
$MA^2 = MB^2 = MC\cdot MD$。这说明,任意做过点 $C, D$ 的 $\odot \Gamma$ 及与直线 $l$ 相切于点 $B$ 的 $\odot O$,则点 $M$ 对 $\odot \Gamma, \odot O$ 的幂相等,即其在 $\odot \Gamma, \odot O$ 的根轴上。
证明非常显然。
【性质1.6】
如下图,$\triangle{ABC}$ 的内切圆 $\odot I$ 与三边分别切于 $D, E, F$,直线 $EF, BC$ 交于点 $P$,则 $B, C, D, P$ 成调和点列。
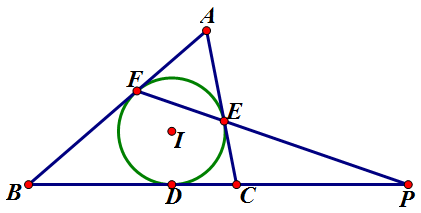
对 $\triangle{ABC}$ 及其截线 $FEP$ 用 Menelaus 定理得$\dfrac{AF}{FB}\cdot\dfrac{BP}{PC}\cdot\dfrac{CE}{EA} = 1$。
又 $AE = AF, BF = BD, CE = CD$,故 $\dfrac{BD}{DC} = \dfrac{BP}{PC}$,根据【定义1.1】$B, C, D, P$ 成调和点列。
调和线束
【定义2.1】
若一条直线上的点 $A, B, C, D$ 为一组调和点列,点 $P$ 不在直线上,连接 $PA, PB, PC, PD$,则 $PA, PB, PC, PD$ 为一组调和线束。
【性质2.1】
对于直线 $l$ 上顺序四点 $A, C, B, D$ 与直线 $l$ 外一点 $P$,则 $\dfrac{\sin\angle{APC}}{\sin\angle{BPC}}=\dfrac{\sin\angle{APD}}{\sin\angle{BPD}}$ 等价于 $A, B, C, D$ 成调和点列。
$A, B, C, D$ 成调和点列 $\iff \dfrac{AC}{BC} = \dfrac{AD}{BD}$
而 $\dfrac{AC}{BC} = \dfrac{PA\sin\angle{APC}}{PB\sin\angle{BPC}}, \dfrac{AD}{BD} = \dfrac{PA\sin\angle{APD}}{PB\sin\angle{BPD}}$
故 $\dfrac{\sin\angle{APC}}{\sin\angle{BPC}}=\dfrac{\sin\angle{APD}}{\sin\angle{BPD}}\iff\dfrac{AC}{BC} = \dfrac{AD}{BD}$,证毕。
在一些地方【性质2.1】被作为调和线束的定义,但本处我们用调和点列来定义调和线束。
【性质2.2】
对于调和点列 $PA, PB, PC, PD$,作不过 $P$ 的另一直线截该调和点列于点 $A’, B’, C’, D’$,则 $A’, B’, C’, D’$ 也为调和点列。
观察到【性质2.1】仅与 $PA, PB, PC, PD$ 四条直线间夹角有关而与直线 $l$ 的选取无关,故显然正确。
【性质2.3】
对于直线 $l$ 上顺次四点 $A, C, B, D$ 及直线 $l$ 外一点 $P$,以下四个条件中任意两个可推出另外两个:
- $A, B, C, D$ 成调和点列;
- $CP\perp PD$;
- $PC$ 平分 $\angle{APB}$;
- $PD$ 平分 $\angle{APB}$ 外角。
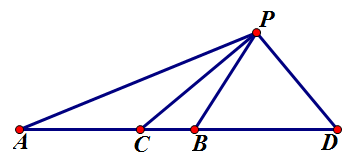
均较显然,以下仅给出1,2推3,4及3,4推1,2的证明。
1,2推3,4:
由1,2知 $\dfrac{\sin\angle{APC}}{\sin\angle{BPC}}=\dfrac{\sin\angle{APD}}{\sin\angle{BPD}} = \dfrac{\sin(\frac{\pi}{2}+\angle{APC})}{\sin(\frac{\pi}{2}-\angle{BPC})}=\dfrac{\cos\angle{APC}}{\cos\angle{BPC}}$,易得3,4。
3,4推1,2:
2显然成立。
由3知 $\dfrac{AC}{BC}=\dfrac{S_{\triangle{APC}}}{S_{\triangle{BPC}}}=\dfrac{AP}{BP}$
由4知 $\dfrac{AD}{BD}=\dfrac{S_{\triangle{APD}}}{S_{\triangle{BPD}}}=\dfrac{AP}{BP}$
故 $\dfrac{AC}{BC}=\dfrac{AD}{BD}$,得证。
调和四边形
【定义3.1】
设 $ABCD$ 为圆内接四边形,若满足 $AB\cdot CD = AD\cdot BC$,则称四边形 $ABCD$ 为调和四边形。
【性质3.1】
$ABCD$ 为 $\odot O$ 的内接四边形,则过 $A, C$ 作切线 $PA, PC$,且 $P, B, D$ 共线为 $ABCD$ 是调和四边形的充分必要条件。
【性质3.2】
$ABCD$ 为 $\odot O$ 的内接四边形,则取 $\odot O$ 上任意一点 $P$,$PA, PB, PC, PD$ 为调和线束为 $ABCD$ 是调和四边形的充分必要条件。
极点与极线
设 $\odot O$ 半径为 $R$。
【定义4.1】
对于不同于 $\odot O$ 的任意一点 $P$,作一直线 $l$ 通过 $P$ 的反演像 $P’$(即 $O, P, P’$ 共线且 $OP\cdot OP’ = R^2$)且垂直于射线 $OP$,则称直线 $l$ 为点 $P$ 的极线,点 $P$ 为直线 $l$ 的极点。
【性质4.1】
显然,对于 $\odot O$ 外的一点 $P$,做切线 $PQ_1, PQ_2$,则 $P$ 的极线为 $Q_1Q_2$。
【性质4.2】
(配极定理)若点 $A$ 的极线穿过点 $D$,则点 $D$ 的极线也穿过点 $A$,一般称 $A, D$ 互为共轭点。设 $\operatorname{cp}(A, \odot O)$ 为点 $A$ 对 $\odot O$ 的幂,则此时有 $AD^2 = \operatorname{cp}(A, \odot O) + \operatorname{cp}(D, \odot O)$。
陪位中线
阿波罗尼斯圆
稍微深入些的性质
回到内切圆构型
以下构型在内切圆基础上延伸。
【性质5.1】
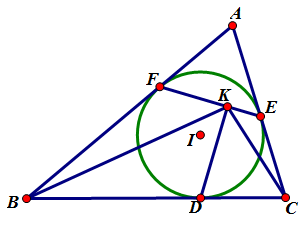
如图,过点 $D$ 作 $EF$ 的垂线,垂足为 $K$,则 $DK$ 平分 $\angle{BKC}$。
由【性质1.6】与【性质2.3】既得。
【性质5.2】
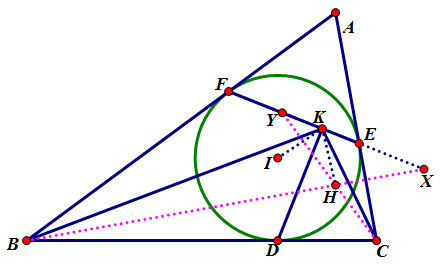
在上图的基础上,$H$ 是 $\triangle{ABC}$ 垂心,则直线 $KH$ 与 $KI$ 关于直线 $KD$ 对称。
设直线 $BH, EF$ 交于 $X$,直线 $CH, EF$ 交于 $Y$。
由【性质5.1】易得 $\triangle{BFK}\sim\triangle{CEK}$
由于 $BX\parallel IE, CY\parallel IF$,故 $\triangle{EIF}\sim\triangle{YHX}$
且知 $\triangle{BFX}\sim\triangle{CEY}\Rightarrow\dfrac{FX}{EY}=\dfrac{BF}{CE}=\dfrac{FK}{EK}=\dfrac{FX-FK}{EY-EK}=\dfrac{KX}{KY}$
则 $\triangle{EIF}\sim\triangle{YHX}$,且 $K$ 与 $K$ 是对应点,故 $\angle{FKI}=\angle{EKH}$
又 $DK\perp EF$,故直线 $KH$ 与 $KI$ 关于直线 $KD$ 对称
($I, H$ 未必在直线 $EF$ 的同一侧,但以上证明对于是否在同一侧均适用)