「AGC022E」Median Replace

发表于 | 更新于 | 分类于 | 阅读次数：

这是毕克好久之前讲过的题……当时没写，现在再看到，回忆起做法就写了一发。

题意简述

[AGC 022E]

定义长度为 $n$（奇数）的 01 字符串是好的，当且仅当可以通过进行 $\frac{n - 1}{2}$ 次下面的变换，使得最后字符串变为 1 。

变换是选择一个长度为 $3$ 的字串，将其改为这 $3$ 个字符的众数（即每次操作会减少 $2$ 个字符）。

先有一个字符串 $S$ ，保证长度为奇数，只含有 0, 1, ? 。分别将每个 ? 改为 0 与 1 中的一种，问有多少种方案，使得字符串是好的。

$1\le |S|\le 3\times 10^5$ 。

主要思路

可以发现，如果在字符串后面加入一个字符，某些操作是不劣的。比如 000 肯定先变成 0 ，011 或 101 肯定先变成 1 。

然后我们可以构造出如下的自动机。

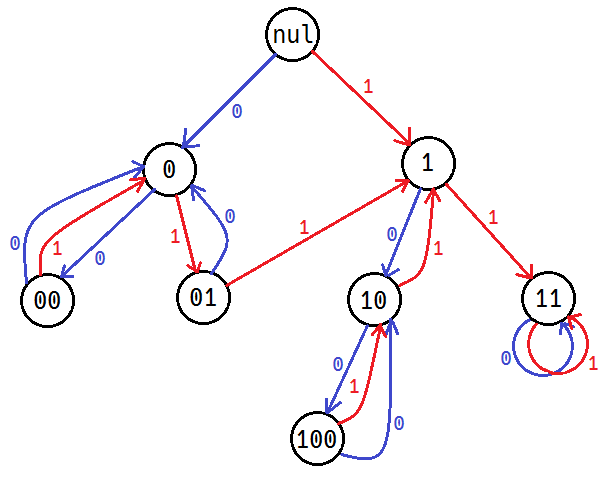
至于为啥 11 只加一个字符就可以再次变为 11 ，你可以理解为 11 后面无论加入什么，最后总是好的。

然后就可以倒着 dp 了。

参考代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include<bits/stdc++.h>
namespace my_std{
    using namespace std;
    #define reg register
    #define Rint register int
    #define FOR(i,a,b) for(register int i=(a),ed_##i=(b);i<=ed_##i;++i)
    #define ROF(i,a,b) for(register int i=(a),ed_##i=(b);i>=ed_##i;--i)
    #define FORit(templ,arr,i,a,b) for(register templ *i=(arr)+(a),*ed_##i=(arr)+(b)+1;i!=ed_##i;++i)
    #define ROFit(templ,arr,i,a,b) for(register templ *i=(arr)+(a),*ed_##i=(arr)+(b)-1;i!=ed_##i;--i)
    #define GO(x,p,e,i,v) for(register int i=p[x].head,v;i;i=e[i].link)
    #define MEM(x,v) memset(x,v,sizeof(x))
    #define fir first
    #define sec second
    #define pq priority_queue
    #define MP make_pair
    typedef long long LL;
    typedef double DB;
    typedef pair<int,int> PII;
    #define Templ(T) template<typename T>
    inline int read(){
        reg int ans=0,f=1; reg char c=getchar();
        while(!isdigit(c)) f^=(c=='-'), c=getchar();
        for(;isdigit(c);c=getchar()) ans=(ans<<1)+(ans<<3)+(c^48);
        return f?ans:-ans;
    }
    Templ(_Tp) inline int chkmin(_Tp &x,_Tp y){ return x>y?x=y,1:0; }
    Templ(_Tp) inline int chkmax(_Tp &x,_Tp y){ return x<y?x=y,1:0; }
    #define using_mod
    const int mod = 1000000007;
    #ifdef using_mod
    inline void inc(int &x, const int &y){ x += y; if(x >= mod) x -= mod; }
    inline void dec(int &x, const int &y){ x -= y; if(x < 0) x += mod; }
    inline int ksm(int x,LL y){ int res=1; for(;y;y>>=1,x=1ll*x*x%mod) if(y&1) res=1ll*res*x%mod; return res;}
    #endif
    Templ(_Tp) inline _Tp gcd(_Tp x,_Tp y){ return y?gcd(y,x%y):x; }
    inline int VSC_Local(){
        #ifdef VSC_Compile
        while(getchar() != '\n');
        #endif
        return 0;
    }
    #define FILE(s) freopen(s ".in", "r", stdin), freopen(s ".out", "w", stdout)
    #define PBTXDY
}
using namespace my_std;

/*
 * null + '0' -> "0", null + '1' -> "1"
 * "0" + '0' -> "00", "0" + '1' -> "01"
 * "1" + '0' -> "10", "1" + '1' -> "11"
 * "00" + '0' -> "0", "00" + '1' -> "0"
 * "01" + '0' -> "0", "01" + '1' -> "1"
 * "10" + '0' -> "100", "10" + '1' -> "1"
 * "11" + '0' -> "11", "11" + '1' -> "11"
 * "100" + '0' -> "10", "100" + '1' -> "10"
*/
const int N = 300010, trans[8][2] = {{1, 2}, {3, 4}, {5, 6}, {1, 1}, {1, 2}, {7, 2}, {6, 6}, {5, 5}};
int n, dp[N][8];
char sc[N];

int main(){
    scanf("%s", sc);
    n = strlen(sc);
    dp[n][2] = dp[n][6] = 1;
    ROF(i, n - 1, 0){
        FOR(t, 0, 7){
            if(sc[i] != '0') inc(dp[i][t], dp[i + 1][trans[t][1]]);
            if(sc[i] != '1') inc(dp[i][t], dp[i + 1][trans[t][0]]);
        }
    }
    printf("%d\n", dp[0][0]);
    return VSC_Local();
}