「AGC039D」Incenters

发表于 | 更新于 | 分类于 | 阅读次数：

粉兔的题解令我学到许多……

题意简述

[AGC 039D]

给定单位圆上的 $n$ 个点 $(\cos(\dfrac{2\pi T_i}{L}), \sin(\dfrac{2\pi T_i}{L}))$ 。求等概率随机三个不同的点的内心的期望位置。
$3\le n\le 3000, n\le L\le 10^9, 0\le T_i < T_{i + 1}\le L - 1$ 。

主要思路

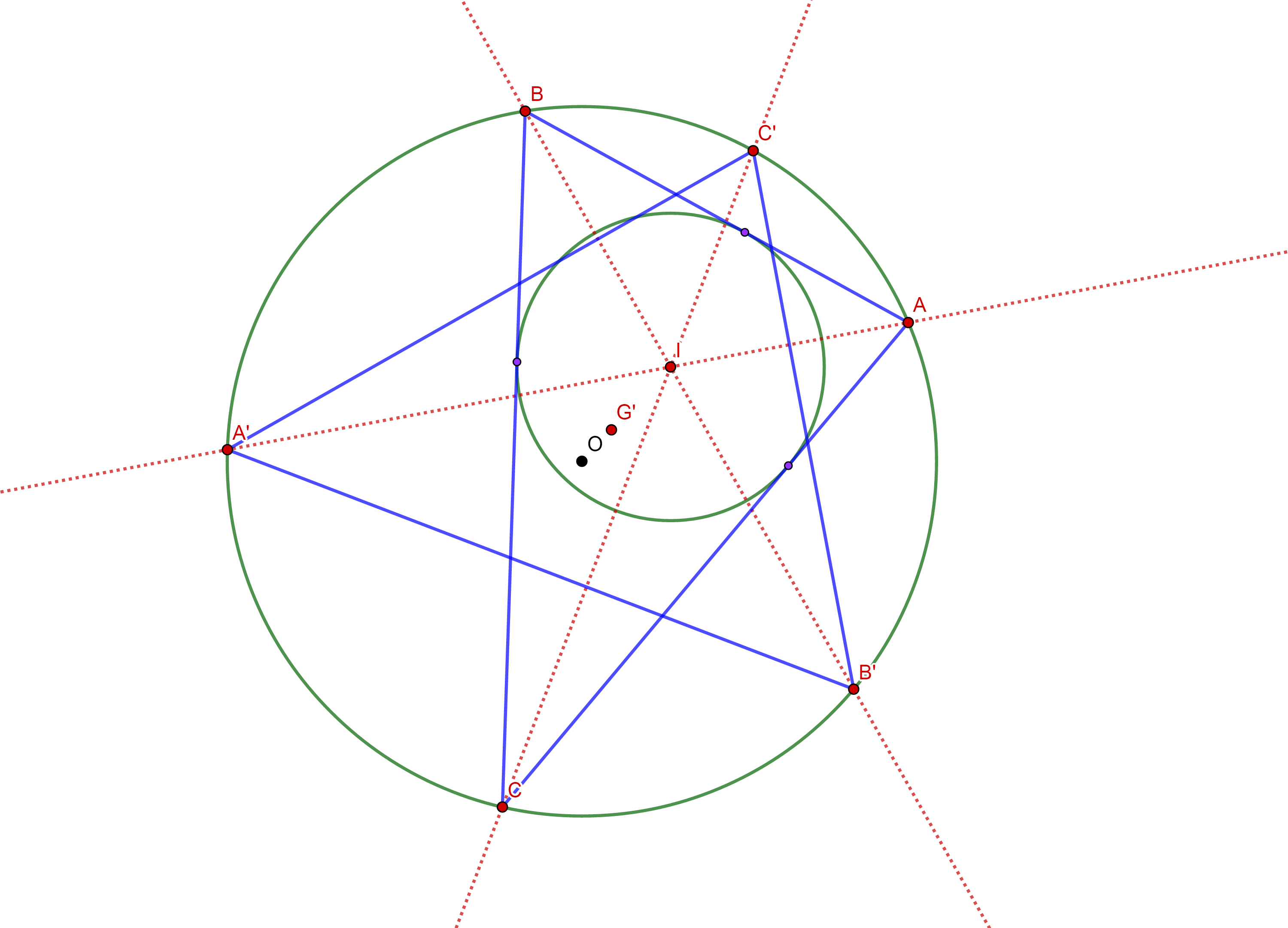
如图，$\triangle{ABC}$ 的外心为 $O$ ，内心为 $I$ 。

分别延长 $AI, BI, CI$ 与 $\odot O$ 交于点 $A^\prime, B^\prime, C^\prime$ 。则易得 $A^\prime, B^\prime, C^\prime$ 分别为弧 $\overset{\LARGE{\frown}}{BC}, \overset{\LARGE{\frown}}{CA}, \overset{\LARGE{\frown}}{AB}$ （不经过 $A, B, C$ 的那一段）的中点。

根据鸡爪定理，有 $A^\prime I = A^\prime C, B^\prime I = B^\prime C$ ，所以 $IC\!\perp\!A^\prime B^\prime$ ，即 $IC^\prime\!\perp\!A^\prime B^\prime$ 。所以 $I$ 同时为 $\triangle{A^\prime B^\prime C^\prime}$ 的垂心 $H^\prime$ 。

根据欧拉线定理，有 $\overrightarrow{OH^\prime} = 3\overrightarrow{OG^\prime} = \overrightarrow{OA^\prime} + \overrightarrow{OB^\prime} + \overrightarrow{OC^\prime}$ 。

所以求 $E(I) = E(H^\prime)$ 只用求 $E(A^\prime) + E(B^\prime) + E(C^\prime)$ 即可。

这个枚举点对计算即可，复杂度 $O(n^2)$ 。

参考代码

真的很短……
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;
#define reg register
#define Rint register int
#define FOR(i,a,b) for(register int i=(a),ed_##i=(b);i<=ed_##i;++i)
#define ROF(i,a,b) for(register int i=(a),ed_##i=(b);i>=ed_##i;--i)
typedef double DB;
inline int read(){
    reg int ans=0,f=1; reg char c=getchar();
    while(!isdigit(c)) f^=(c=='-'), c=getchar();
    for(;isdigit(c);c=getchar()) ans=(ans<<1)+(ans<<3)+(c^48);
    return f?ans:-ans;
}

const DB pi = acos(-1);
const int N = 3010;
int n, L, t[N];
DB ansx, ansy;

int main(){
    n = read(), L = read();
    FOR(i, 1, n) t[i] = read();
    reg DB x, y, res = n * (n - 1.0) * (n - 2.0) / 6.0;
    FOR(A, 1, n - 1) FOR(B, A + 1, n){
        x = cos(pi * (t[A] + t[B]) / L);
        y = sin(pi * (t[A] + t[B]) / L);
        ansx += x * (n - 2 * (B - A));
        ansy += y * (n - 2 * (B - A));
    }
    printf("%.12lf %.12lf\n", ansx / res, ansy / res);
    return 0;
}