nantf 由于生病窝在家里打 Global Round 6 然后 rating 超过 p_b_p_b 了……
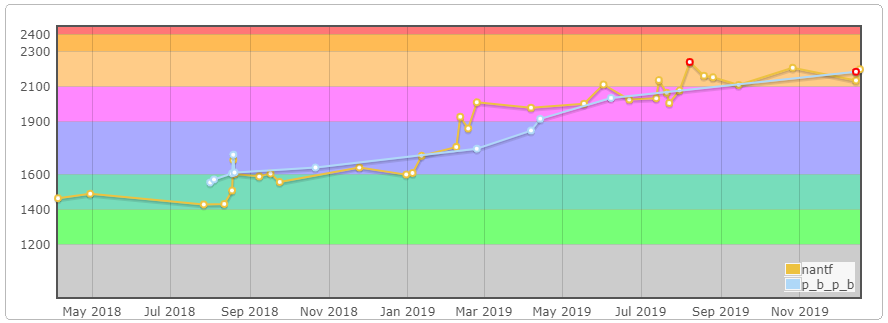
然后他场上做了 A - E。
题意简述
给定一棵树大小为 $n$ 。定义一个点集 $S$ 是 $k$ 均匀的,当且仅当对于任意 $u,v\in S, u\ne v$ ,有 $\operatorname{dist}(u, v) = k$ 或 $\operatorname{dist}(u, v) = k + 1$ ,其中 $\operatorname{dist}(u, v)$ 表示 $u$ 与 $v$ 在树上的距离,即它们的简单路径上的边数。
现在希望你对于 $1\le k\le n$ ,求出 $k$ 均匀点集点数的最大值。$2 \le n \le 5\times 10^5$ 。
主要思路
题解讲得很迷,然后看了300iq的代码才明白的。
设 $ans[k]$ 为 $k$ 均匀点集点数的最大值。
显然我们可以 dfs 求出最长链的长度 $mxl$ , $k > mxl$ 则 $ans[k] = 1$ , $k \le mxl$ 则 $ans[k] \ge 2$ 。
称一棵有根树的最深深度为根节点到所有叶子节点的距离最大值。
- 对于 $k = 2l + 1$ ($l > 1$) ,最大 $k$ 均匀集必定以一个点 $r$ 为“中心”(该点不在均匀集中),而所有均匀集中的点 $x$ 距离 $r$ 为 $l + 1$ 或 $l$ ,且距离为 $l$ 的点的数量不超过 $1$ 个。
- 对于 $k = 2l$ ($l > 1$) ,也类似,不过较为复杂。可能是以一个点 $r$ 为“中心”,此时所有均匀集中的点 $x$ 距离 $r$ 为 $l$ ;也可能是以一条边 $(s, t)$ 为“中心”,此时所有均匀集中的点 $x$ 有 $\min(\operatorname{dist}(x, s), \operatorname{dist}(x, t)) = l$ 。
由上,可得 $ans[k] \ge ans[k + 2]$ 。
对于 $k$ 为奇数,或 $k$ 为偶数的第一种情况,我们可以对每个点 $u$ ,求出若这棵树以这个点为根,它每个儿子的子树最深深度,并降序排序存入数组 $ret$ 中。
这样,我们就可以 $O(n\log_2 n)$ 地获得上述情况的答案。
这部分非常好写,但是对于 $k$ 为偶数且以一条边为“中心”的情况无法处理。
对于这种情况,我们对每个点 $u$ ,枚举其儿子 $v$ 。然后对于 $v$ 也求出它每个儿子的子树最深深度(不包含 $u$ ),并降序存入数组 $tmp$ 中。
然后对于每个 $ret[i], tmp[i]$ ,用类似上述的方法来更新。
这里每个节点会被访问两次,所以总的时间复杂度还是 $O(n\log_2 n)$ 。
参考代码
上面的东西都可以两次 dfs 搞定。
1 |
|
顺便从300iq那里学来了一个东西。
1 | struct BIT{ |
这个东西可以支持单点修改和查询后缀和。证明正确性和复杂度的方法好像和普通树状数组差不多。