然而能看懂的东西不多
前置知识
给定 $\triangle{ABC}$ 与其外接圆 $\odot{\Omega}$ ,$\triangle{ABC}$ 的 $A-$伪内切圆 $\odot{\omega_A}$ 分别切 $\odot{\Omega}, AC, AB$ 于点 $T, E, F$ 。$I$ 为 $\triangle{ABC}$ 内心,$N, M$ 分别为 $\overset{\LARGE{\frown}}{AB}, \overset{\LARGE{\frown}}{AC}$ 中点。$AT$ 交 $\odot{\omega_A}$ 于点 $P$ 。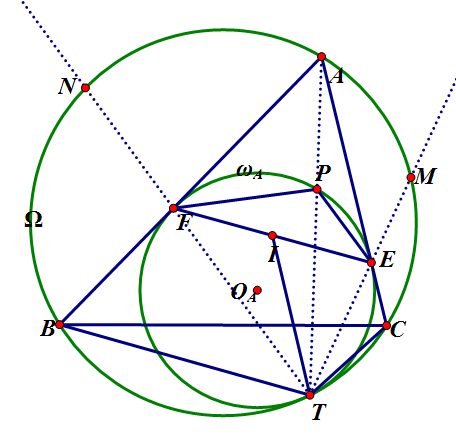
有以下几个经典结论:
- $I, E, F$ 共线且 $EI = FI$ 。
- $N, F, T$ 共线, $M, E, T$ 共线。
- $\angle{BTI} = \angle{CTI}$ 。
- $TBFI\sim TFPE\sim TIEC$ 。
例题
A
给定 $\triangle{ABC}$ 与其外接圆 $\odot{O}$ ,三个伪内切圆 $\odot{O_A}, \odot{O_B}, \odot{O_C}$ 分别切 $\odot{O}$ 于点 $T_A, T_B, T_C$ 。
证明 $AT_A, BT_B, CT_C$ 共点。
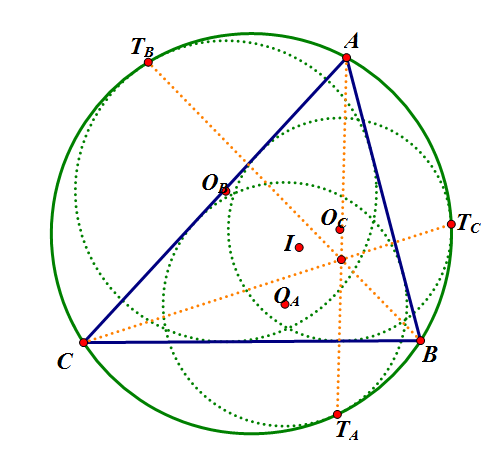
A-sol
只需证 $\dfrac{AT_B}{T_BC}\dfrac{CT_A}{T_AB}\dfrac{BT_C}{T_CA} = 1$ 。
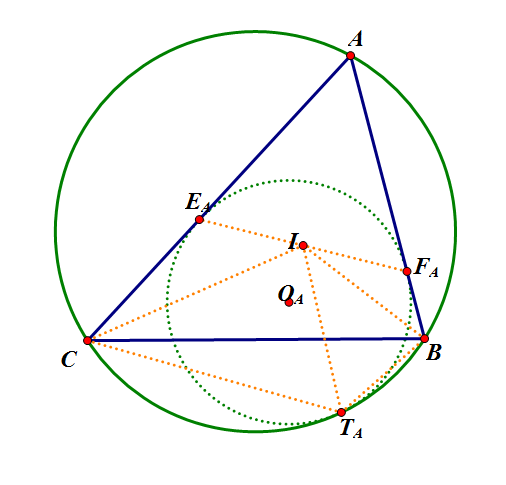
不妨只看 $\dfrac{CT_A}{BT_A}$ 。
由 Mannheim 定理易证 $\triangle{BIT_A}\sim \triangle{ICT_A}$ ,即有 $\dfrac{BI^2}{CI^2} = \dfrac{BT_A}{IT_A}\times \dfrac{IT_A}{CT_A} = \dfrac{BT_A}{CT_A}$ 。
所以 $\dfrac{AT_B}{T_BC}\dfrac{CT_A}{T_AB}\dfrac{BT_C}{T_CA} = 1$ ,证毕。
B
给定 $\triangle{ABC}$ 外接圆 $\odot{\Omega}$ ,过 $A$ 作 $AA^\prime\parallel BC$ 交外接圆于点 $A^\prime$ ,$L$ 为 $\overset{\LARGE{\frown}}{BAC}$ 的中点。 $\triangle{ABC}$ 内切圆 $\odot{I}$ 与 $BC$ 切于点 $D$ 。
射线 $A^\prime D, LI$ 交于点 $T$,证明 $T$ 在 $\odot{\Omega}$ 上。
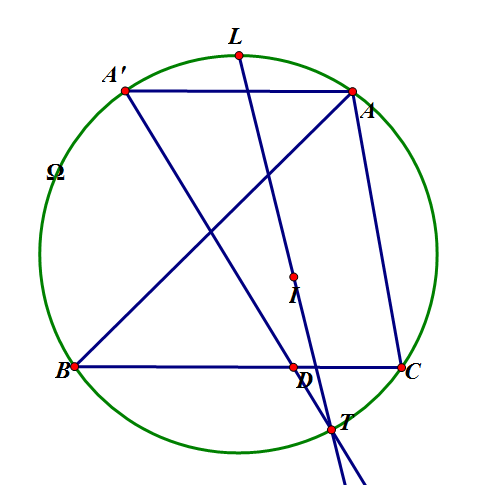
B-sol
作 $\triangle{ABC}$ 的 $A-$伪内切圆 $\odot{\omega_A}$ ,切点分别为 $F, E, T$ 。设点 $N$ 为 $AT$ 与 $BC$ 交点。
下证 $TI$ 延长线与 $\odot{\Omega}$ 交于 $L$ 为 $\overset{\LARGE{\frown}}{BAC}$ 的中点, $TD$ 延长线交 $\odot{\Omega}$ 于点 $A^\prime$ 且 $A^\prime A\parallel BC$ 。
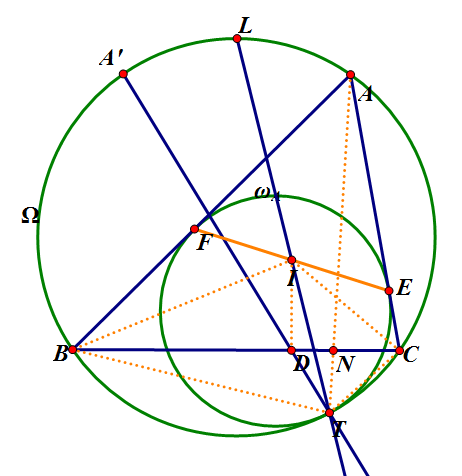
证明 $L$ 为 $\overset{\LARGE{\frown}}{BAC}$ 中点
由 Mannheim 定理,显然 $TF$ 延长线过 $\overset{\LARGE{\frown}}{AB}$ 的中点,即有 $\angle{BTF} = \dfrac{C}{2}$ 。又 $\angle{FIB} = \angle{BIA} - \dfrac{\pi}{2} = \dfrac{C}{2} = \angle{BTF}$ ,可得 $B, T, I, F$ 共圆。同理得 $C, T, I, E$ 共圆。倒角,显然有 $BFIT\sim IECT$ 。
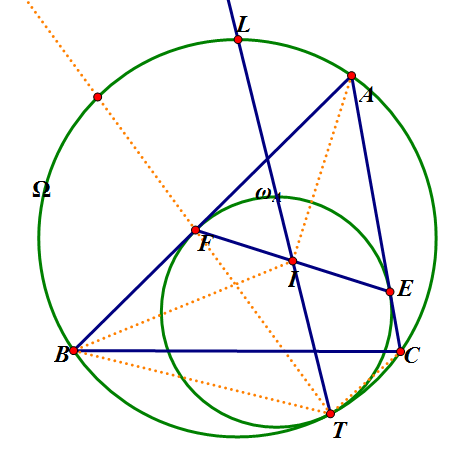
故 $\angle{BTI} = \angle{CTI} = \dfrac{\pi - A}{2}$ ,得证。
证明 $AA^\prime\parallel BC$

原命题等价于证明 $TL$ 为 $\angle{DTN}$ 角平分线,即 $\angle{BTD} = \angle{CTN}$。
注意到此时有 $\dfrac{BD}{CD} = \dfrac{BT\sin\angle{BTD}}{CT\sin\angle{CTD}}, \dfrac{BN}{CN} = \dfrac{BT\sin\angle{BTN}}{CT\sin\angle{CTN}}$ ,即 $\dfrac{BD}{CD}\times \dfrac{BN}{CN} = \dfrac{BT^2}{CT^2}$ 。易证上式也为为 $\angle{BTD} = \angle{CTN}$ 的充分条件。
导面积:
$\dfrac{BN}{CN} = \dfrac{S_{\triangle{ABT}}}{S_{\triangle{ACT}}} = \dfrac{AB\times BT}{AC\times CT}$ 。
导边:
$\dfrac{BD}{CD} = \dfrac{BI\sin\angle{BID}}{CI\sin\angle{CID}} = \dfrac{BI\sin{\frac{\pi + B}{2}}}{CI\sin\frac{\pi + C}{2}}$
注意到 $\triangle{ABI}, \triangle{ACI}$ 中有 $\dfrac{AB}{AC} = \dfrac{BI\sin\angle{\frac{\pi + C}{2}}}{CI\sin\angle{\frac{\pi + B}{2}}}$ ,所以有 $\dfrac{BD}{CD} = \dfrac{BI^2}{CI^2}\times \dfrac{AC}{AB}$ 。
利用上一题的结论可得 $\dfrac{BD}{CD} = \dfrac{BT}{CT}\times \dfrac{AC}{AB}$ 。
$\therefore \dfrac{BD}{CD} \times \dfrac{BN}{CN} = \dfrac{BT^2}{CT^2}$ ,得证。