题意简述
给你一个长为 $n$ 的 AB 字符串。假设一个球从某一个方向（左或右）到达了一个 A ，该位置将变为 B 且该球会反弹；到达了一个 B ，该位置将变为 A 且该球会穿过该位置。
现在从字符串的最左边扔进去 $k$ 个球，每个球都在上一个球已经弹出字符串之后再放入（可以证明，任何字符串都不能把球永远留在字符串中）。
求最后的字符串。
$1\le n\le 200000, 1\le k\le 10^9$ 。
「CF1266F」Almost Same Distance
nantf 由于生病窝在家里打 Global Round 6 然后 rating 超过 p_b_p_b 了……
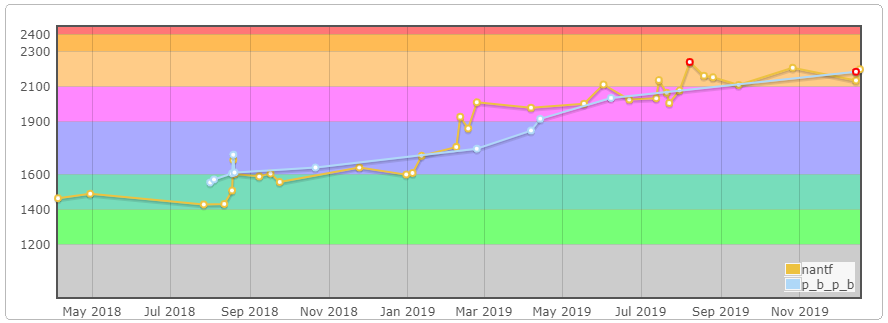
然后他场上做了 A - E。
题意简述
给定一棵树大小为 $n$ 。定义一个点集 $S$ 是 $k$ 均匀的，当且仅当对于任意 $u,v\in S, u\ne v$ ，有 $\operatorname{dist}(u, v) = k$ 或 $\operatorname{dist}(u, v) = k + 1$ ，其中 $\operatorname{dist}(u, v)$ 表示 $u$ 与 $v$ 在树上的距离，即它们的简单路径上的边数。
现在希望你对于 $1\le k\le n$ ，求出 $k$ 均匀点集点数的最大值。$2 \le n \le 5\times 10^5$ 。
「Ynoi2015」我回来了
这个题主要是当做手写 bitset 板子来写的。
Idea：lxl Solution：lxl Std：lxl Data：lxl
对这题的评价：1/11
大概是 lxl 评价最低的题吧……
题意简述
珂朵莉给你一个无向图，每次查询的时候给一堆二元组 $(x_i,y_i)$ 。
求图中有多少个点 $u$ 与至少一个这次询问给出的二元组 $(x_i,y_i)$ 满足 $dist(u,x_i) \le y_i$ ，其中 $dist(u, v)$ 表示 $u, v$ 这两个点在图中的距离（不连通为 $\inf$），边权全为 $1$ 。
记 $n$ 为点数， $m$ 为边数， $q$ 为询问个数， $cnt$ 为给出二元组的总数。
$1\le n\le 10^3, 1\le m, q\le 10^5, cnt \le 2.1 \times 10^6$ 。
「Ynoi2015」盼君勿忘
「Ynoi2015」纵使日薄西山
感觉失去卡常的兴致了……，虽然这个题明明不卡常。
Idea：ccz Solution：ccz Std：ccz Data：ccz
对这题的评价：3/11
题意简述
维护一个长度为 $n$ 的正整数序列 $a$ ， $m$ 次修改序列中某个位置的值。
每次修改后问对序列重复进行以下操作，需要进行几次操作才能使序列变为全 $0$ （询问后序列和询问前相同，不会变为全 $0$ ）：
选出序列中最大值的出现位置，若有多个最大值则选位置标号最小的一个，设位置为 $x$ ，则将 $a{x-1},a_x,a_{x+1}$ 的值减 $1$ ，如果序列中存在小于 $0$ 的数，则把对应的数改为 $0$ 。
$1\le n, m\le 10^5, 1\le a_i \le 10^9$ 。
「CF1172D」Nauuo and Portals
ouuan 场的有意思构造题。
题意简述
定义一对传送门 $(A,A^\prime)$ 为从 $A$ 门进入会从 $A^\prime$ 门出来，且保持进入 $A$ 门的方向（从 $A^\prime$ 进去同理）。
给出一个 $n\times n$ ($1\le n\le 10^3$) 的矩形和 $2n$ 个要求，其中前 $n$ 个要求的形式为 $(r_i,n)$ ，代表 $\texttt{Nauuo}$ 从 $(i,1)$ 这个格子出发一直向右走，经过若干对传送门（或者不经过传送门）后从 $(r_i,n)$ 这个格子走出矩形；后 $n$ 个要求的形式为 $(n,c_i)$ ，代表 $\texttt{Nauuo}$ 从 $(1,i)$ 这个格子出发一直向下走，经过若干对传送门（或者不经过传送门）后从 $(n,c_i)$ 这个格子走出矩形。
请你在这个 $n\times n$ 的矩形中放置若干对传送门，使得这 $2n$ 个请求可以同时满足。输出传送门的对数和每对传送门两个门各自的坐标。
保证 $r_i, c_i$ 为 $1$ 到 $n$ 的排列。无解时输出 $-1$ 。
注意：你不需要找到使用传送门最少的方案数，只需要让你给出的方案可以满足题目中给出的要求。